题目
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.
样例
输入:[0,1,0,2,1,0,1,3,2,1,2,1]
答案:6(蓝色部分)

题意
本题就是需要寻找凹下去比旁边低的部分。
对于题意的分析部分比较难,如果能正确分析出题意基本就可以解决了。
题解1
这个解法是官方的解法,主要写一下思路:
对于每一条块,把它左边和右边的块一份为二,分别寻找出它左边和右边最高块的高度,显然它最后加了水的高度就是它左右两遍高度的最大值中小的那个。
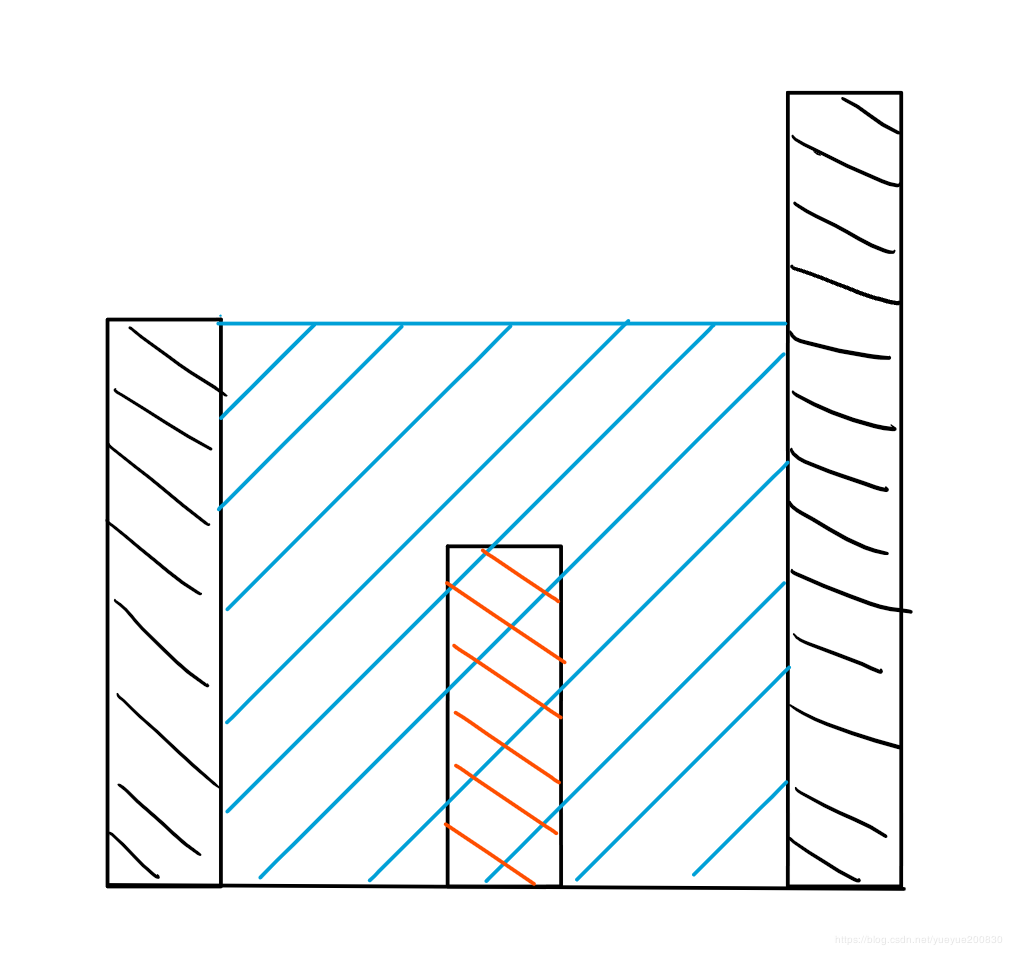
如图红色为随机的一条,两条黑色的是其左右两边最高的两根,显然最后注满的水量至少之蓝色这么多,也就是左右两根黑色中比较矮的那根的长度。
因此sum = sum(min(left_max[i], right_max[i]))
比较普通又方便的一种解法是用dp记录left_max和right_max,时间复杂度和空间复杂度都为O(n)。
而另一种可以更快的方法是用left和right两个来左右一起遍历,同时记录遍历过的left_max和right_max。
只要比较现在遍历过的里面左右的最大值,最大值比较小的那侧现在指向的那块最后的注水量就是那侧遍历到的最大的值。(因为另一侧的最大值一定比这一侧的最大值大)
即,假设现在left_max比right_max小,那么第left个左边所有的值都知道了,最大值为left_max,而它右边的最大值一定会大于等于right_max。因此min(right_max[i], left_max[i]) = left_max[i]。
这样遍历的时间复杂度是O(n)(只需要遍历n次,比dp的2n次少一半),空间复杂度为O(1)(只需要另外4个数记录就好,而dp的额外空间是2n)
附上官方代码:
1 | int trap(vector<int>& height) |
题解2
这个是我绞尽脑汁后的一个比较复杂的解法,时间复杂度O(n),空间复杂度最大O(n)(用stack)
做法是从左往右遍历,遇到可以注水的地方就先把暂时可以注的水给注入。
如样例中有一部分[2,1,0,1,3]
当遇到右侧1的时候,也就是[2,1,0,1]时,在0中注入1的水量,这样就变成了[2,1,1,1]了
当遇到3时,对所有的1都注入1的水量,变成[2,2,2,2,3]。
整个的难点在于用stack的记录,对于同一个高度块只记录一次,每次需要同时记录高度和位置,因此需要用结构体来记录。
又由于是从左往右遍历的,每次记录同高度下最右边的那条。
因为每次遍历完已经填平了所有遍历过的水坑,因此stack中记录的一定是不可以再注入水的,也就是递增或者递减的一堆数。
当每次遇到可以注水的时候,注水量为(mini(left_height, right_height) - current_height)*(left_position-right_position-1)(如有不理解可以考虑一下刚才的example)
1 | struct num{ |
搬运自CSDN:https://blog.csdn.net/yueyue200830/article/details/86755967