非常意外得在一次技术搜索中跳出了foo bar参赛的页面,曾听闻过这是Google的一个特殊招聘渠道,不过感觉近几年这个挑战被宣传后更多得只是一个有趣的挑战,近几年也没见到有人通过这个参与面试了。
Foo Bar一共有5个level的题目,每个level有一个或多个题目,随着level提高,题目的难度也会提高,每个题目都有限制的答题时间,但最短的也有7天,所以可以给答题者足够的思考时间。
题目一共可以用两种语言类回答,Java和Python,因为近期用Python更多些以及Python写起来也更简洁些,所以题解都是用的Python。
Foo Bar类似Google的其他比赛,题目都会有很多的包装,需要阅读理解,个人还是比较欣赏这种没法完全背解答的题目。
另一个比较与众不同的是,这个挑战虽然是一个网页,但全程需要使用命令行进行测试提交挑战,只有在编写代码时是一个web端的编辑器。
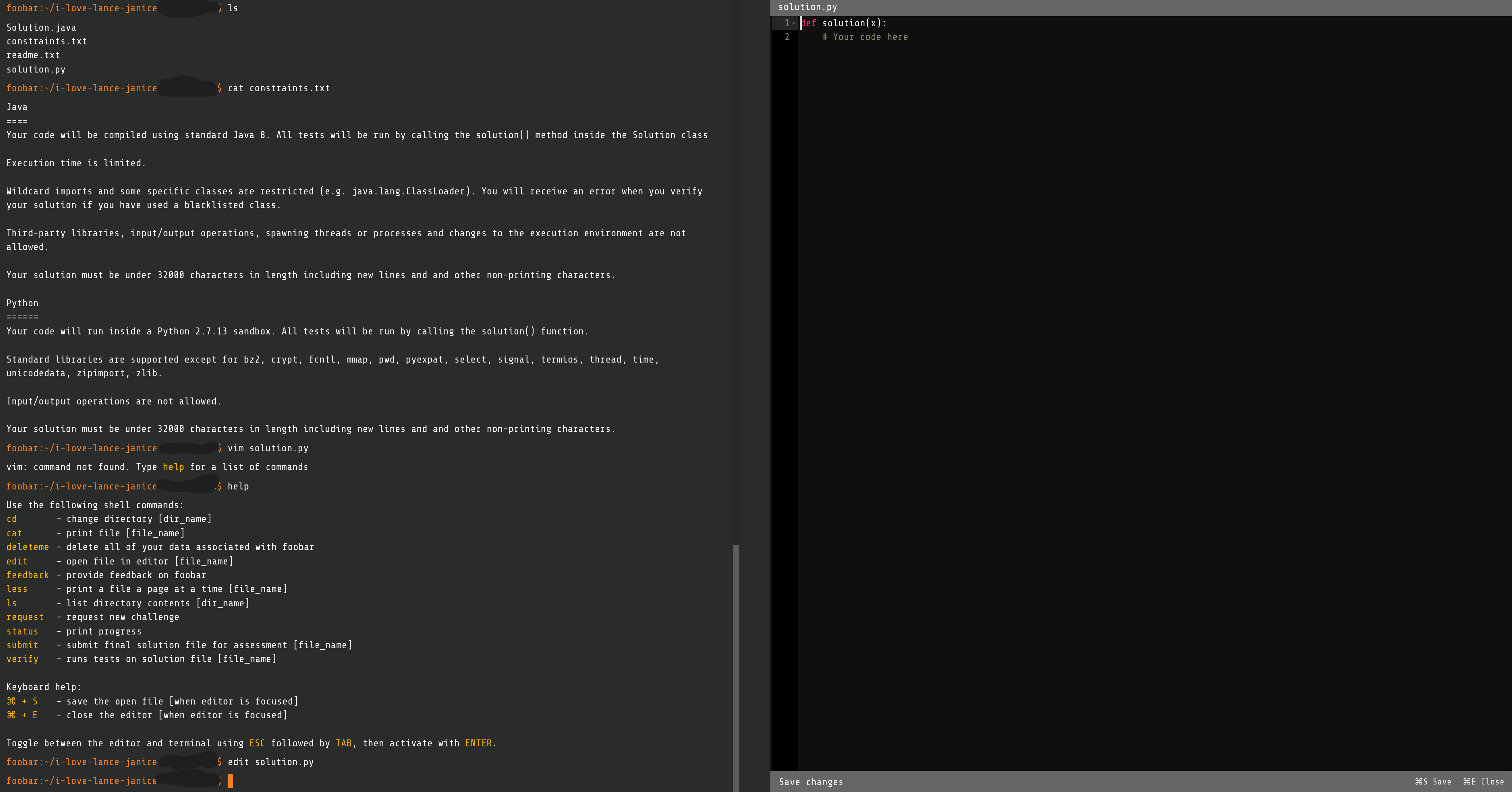
Level 1
level 1只有一题,一开始题目没有复制出来,只有个截图看下吧
Level 1-1
题目
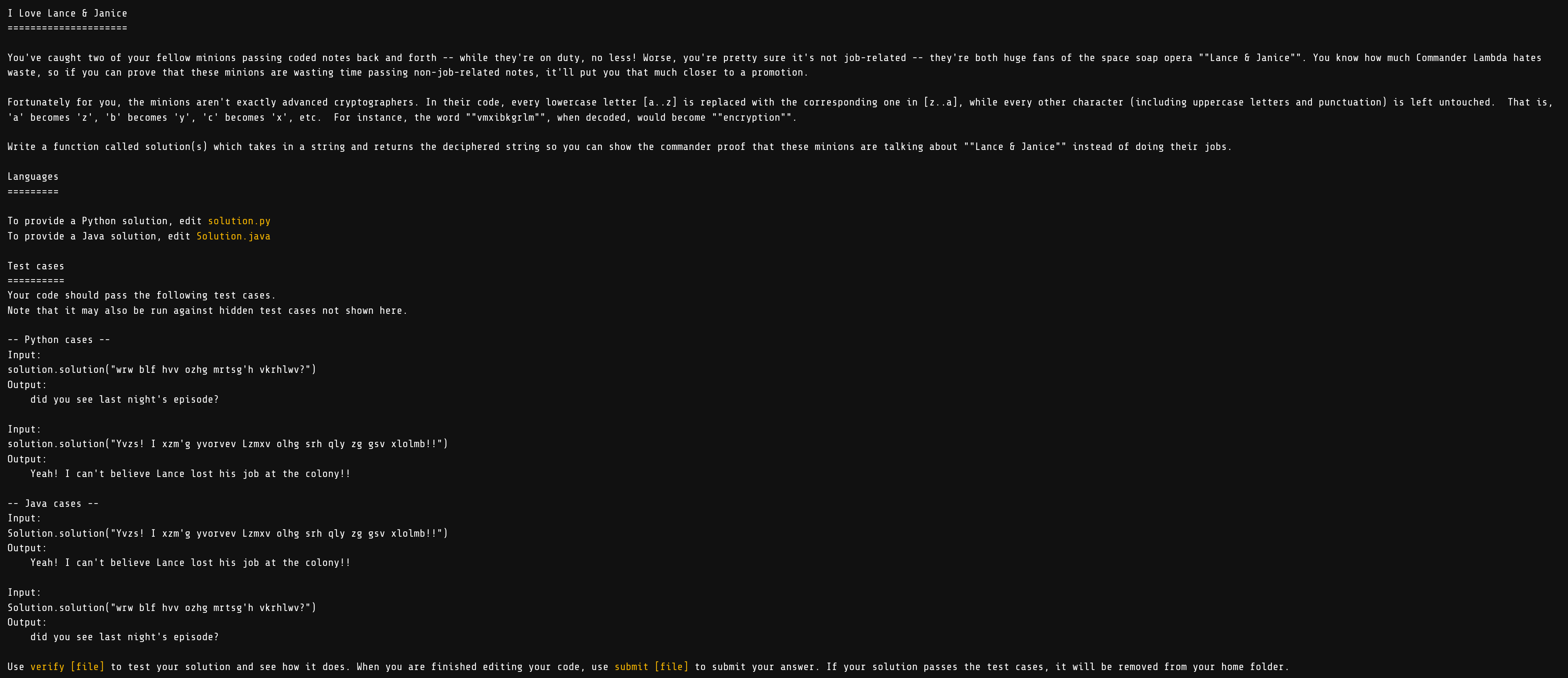
题解
第一题还是非常简单的,做一个字符串的转换就可以了
1 | def solution(x): |
代码通过后会有这么一个可爱的图案
Level 2
level 2有两题,题目总体还是比较简单的
Level 2-1
题目
Please Pass the Coded Messages
You need to pass a message to the bunny workers, but to avoid detection, the code you agreed to use is… obscure, to say the least. The bunnies are given food on standard-issue plates that are stamped with the numbers 0-9 for easier sorting, and you need to combine sets of plates to create the numbers in the code. The signal that a number is part of the code is that it is divisible by 3. You can do smaller numbers like 15 and 45 easily, but bigger numbers like 144 and 414 are a little trickier. Write a program to help yourself quickly create large numbers for use in the code, given a limited number of plates to work with.
You have L, a list containing some digits (0 to 9). Write a function solution(L) which finds the largest number that can be made from some or all of these digits and is divisible by 3. If it is not possible to make such a number, return 0 as the solution. L will contain anywhere from 1 to 9 digits. The same digit may appear multiple times in the list, but each element in the list may only be used once.
测试样例
1 | Input: |
题解
题目整体可以分为两步,1:把数字从大到小排序;2:去掉几个数(0-2个数)是的数字之和模3余0。
关于第二步,很明显去掉一个字符会大于去掉两个字符,且去掉的数字越小越好,所以依次尝试这两种情况是否能满足3的倍数即可。
1 | def solution(l): |
Level 2-2
题目
Power Hungry
Commander Lambda’s space station is HUGE. And huge space stations take a LOT of power. Huge space stations with doomsday devices take even more power. To help meet the station’s power needs, Commander Lambda has installed solar panels on the station’s outer surface. But the station sits in the middle of a quasar quantum flux field, which wreaks havoc on the solar panels. You and your team of henchmen have been assigned to repair the solar panels, but you’d rather not take down all of the panels at once if you can help it, since they do help power the space station and all!
You need to figure out which sets of panels in any given array you can take offline to repair while still maintaining the maximum amount of power output per array, and to do THAT, you’ll first need to figure out what the maximum output of each array actually is. Write a function solution(xs) that takes a list of integers representing the power output levels of each panel in an array, and returns the maximum product of some non-empty subset of those numbers. So for example, if an array contained panels with power output levels of [2, -3, 1, 0, -5], then the maximum product would be found by taking the subset: xs[0] = 2, xs[1] = -3, xs[4] = -5, giving the product 2*(-3)*(-5) = 30. So solution([2,-3,1,0,-5]) will be “30”.
Each array of solar panels contains at least 1 and no more than 50 panels, and each panel will have a power output level whose absolute value is no greater than 1000 (some panels are malfunctioning so badly that they’re draining energy, but you know a trick with the panels’ wave stabilizer that lets you combine two negative-output panels to produce the positive output of the multiple of their power values). The final products may be very large, so give the solution as a string representation of the number.
测试样例
1 | Input: |
题解
求这些数的乘积之和的最大值,对于正数直接相乘即可;对于负数需要选取偶数个相乘;对于0在只有一个负数的时候会选择。
1 | def solution(xs): |
Level 3
level 3中后两题感觉比较简单,但3-1卡了我很久,感觉逻辑非常绕
Level 3-1
题目
Doomsday Fuel
Making fuel for the LAMBCHOP’s reactor core is a tricky process because of the exotic matter involved. It starts as raw ore, then during processing, begins randomly changing between forms, eventually reaching a stable form. There may be multiple stable forms that a sample could ultimately reach, not all of which are useful as fuel.
Commander Lambda has tasked you to help the scientists increase fuel creation efficiency by predicting the end state of a given ore sample. You have carefully studied the different structures that the ore can take and which transitions it undergoes. It appears that, while random, the probability of each structure transforming is fixed. That is, each time the ore is in 1 state, it has the same probabilities of entering the next state (which might be the same state). You have recorded the observed transitions in a matrix. The others in the lab have hypothesized more exotic forms that the ore can become, but you haven’t seen all of them.
Write a function solution(m) that takes an array of array of nonnegative ints representing how many times that state has gone to the next state and return an array of ints for each terminal state giving the exact probabilities of each terminal state, represented as the numerator for each state, then the denominator for all of them at the end and in simplest form. The matrix is at most 10 by 10. It is guaranteed that no matter which state the ore is in, there is a path from that state to a terminal state. That is, the processing will always eventually end in a stable state. The ore starts in state 0. The denominator will fit within a signed 32-bit integer during the calculation, as long as the fraction is simplified regularly.
For example, consider the matrix m:
[
[0,1,0,0,0,1], # s0, the initial state, goes to s1 and s5 with equal probability
[4,0,0,3,2,0], # s1 can become s0, s3, or s4, but with different probabilities
[0,0,0,0,0,0], # s2 is terminal, and unreachable (never observed in practice)
[0,0,0,0,0,0], # s3 is terminal
[0,0,0,0,0,0], # s4 is terminal
[0,0,0,0,0,0], # s5 is terminal
]
So, we can consider different paths to terminal states, such as:
s0 -> s1 -> s3
s0 -> s1 -> s0 -> s1 -> s0 -> s1 -> s4
s0 -> s1 -> s0 -> s5
Tracing the probabilities of each, we find that
s2 has probability 0
s3 has probability 3/14
s4 has probability 1/7
s5 has probability 9/14
So, putting that together, and making a common denominator, gives an answer in the form of
[s2.numerator, s3.numerator, s4.numerator, s5.numerator, denominator] which is
[0, 3, 2, 9, 14].
测试样例
1 | Input: |
题解
这道计算概率的题目把我绕得非常混乱,应该是自己没想清楚做法,感觉目前的解法也不是最优的,所以看看就好。
尝试过的思路:
- [成功] 正向计算,从s0开始dfs,寻找到terminal的概率
- [失败] 反向计算,从terminal开始反着找到可以到达它的node
最后用的第一个方法来计算,通过dfs计算si到各个node的概率,这里比较困难的点是如何定义dfs,我的定义是si到terminal或已经访问过的node的概率
即如果现在是s1之前访问的是s0,terminal是s4和s5,那么dfs(s1)会计算s1到s0、s4、s5的概率,到s1、s2、s3的概率都是0。
这样定义是为了解决dfs遇到循环如何计算概率,我们观察一个case,现在有三个路径(其中s3、s4是terminal):
- s1 -> s2 -> s1
- s1 -> s3
- s1 -> s4
我们可以看到无论循环多少次s1,最终都会到s3或者s4,实际上的概率与不计算循环是一致的,所以在计算si到其他node的概率时,可以把它到自己的概率平分给其他node
在这样的计算逻辑下,对于si而言,对于未访问过的node,我们可以通过上述定义解决循环访问的问题,而对于已经访问过的node,我们会交回这些node自己处理。
在dfs的逻辑下,也就是当dfs到一个访问过的节点时,会计算这个访问过的节点的概率,并返回给上一级;当得到它所有下游节点到其他节点的概率时,把循环到自己的概率部分去掉再平分
此外,因为是概率,所以这里存储的结构会比较复杂,我采用在list最后加上一个数表示分母
update
搜了一下题解,正确做法应该是马尔科夫链,链接有一个超级简洁的python写法。
1 | def solution(m): |
Level 3-2
题目
Fuel Injection Perfection
Commander Lambda has asked for your help to refine the automatic quantum antimatter fuel injection system for the LAMBCHOP doomsday device. It’s a great chance for you to get a closer look at the LAMBCHOP — and maybe sneak in a bit of sabotage while you’re at it — so you took the job gladly.
Quantum antimatter fuel comes in small pellets, which is convenient since the many moving parts of the LAMBCHOP each need to be fed fuel one pellet at a time. However, minions dump pellets in bulk into the fuel intake. You need to figure out the most efficient way to sort and shift the pellets down to a single pellet at a time.
The fuel control mechanisms have three operations:
1) Add one fuel pellet
2) Remove one fuel pellet
3) Divide the entire group of fuel pellets by 2 (due to the destructive energy released when a quantum antimatter pellet is cut in half, the safety controls will only allow this to happen if there is an even number of pellets)Write a function called solution(n) which takes a positive integer as a string and returns the minimum number of operations needed to transform the number of pellets to 1. The fuel intake control panel can only display a number up to 309 digits long, so there won’t ever be more pellets than you can express in that many digits.
For example:
solution(4) returns 2: 4 -> 2 -> 1
solution(15) returns 5: 15 -> 16 -> 8 -> 4 -> 2 -> 1
测试样例
1 | Input: |
题解
把数字转换成二进制看,末尾有三种情况:
- 末尾是0,直接除2,一次操作,长度少一位
- 末尾仅有一个连续的1,减1除2,两次操作,长度减少一位
- 末尾有n(n>1)个连续的1,加1除2,两次操作,长度减少n位
update
解答应该有问题,估计没有保存最新的代码
1 | def solution(n): |
Level 3-3
题目
Find the Access Codes
In order to destroy Commander Lambda’s LAMBCHOP doomsday device, you’ll need access to it. But the only door leading to the LAMBCHOP chamber is secured with a unique lock system whose number of passcodes changes daily. Commander Lambda gets a report every day that includes the locks’ access codes, but only the Commander knows how to figure out which of several lists contains the access codes. You need to find a way to determine which list contains the access codes once you’re ready to go in.
Fortunately, now that you’re Commander Lambda’s personal assistant, Lambda has confided to you that all the access codes are “lucky triples” in order to make it easier to find them in the lists. A “lucky triple” is a tuple (x, y, z) where x divides y and y divides z, such as (1, 2, 4). With that information, you can figure out which list contains the number of access codes that matches the number of locks on the door when you’re ready to go in (for example, if there’s 5 passcodes, you’d need to find a list with 5 “lucky triple” access codes).
Write a function solution(l) that takes a list of positive integers l and counts the number of “lucky triples” of (li, lj, lk) where the list indices meet the requirement i < j < k. The length of l is between 2 and 2000 inclusive. The elements of l are between 1 and 999999 inclusive. The solution fits within a signed 32-bit integer. Some of the lists are purposely generated without any access codes to throw off spies, so if no triples are found, return 0.
For example, [1, 2, 3, 4, 5, 6] has the triples: [1, 2, 4], [1, 2, 6], [1, 3, 6], making the solution 3 total.
测试样例
1 | Input: |
题解
遍历每个数,将它定为三个数的中间的数lj,找到li和lk的数量,相乘即是满足条件的数
1 | def solution(l): |
Level 4
level 4整体感觉比较难的,第一题是常规算法中不常见的网络流,第二题不确定dfs
Level 4-1
题目
Escape Pods
You’ve blown up the LAMBCHOP doomsday device and relieved the bunnies of their work duries — and now you need to escape from the space station as quickly and as orderly as possible! The bunnies have all gathered in various locations throughout the station, and need to make their way towards the seemingly endless amount of escape pods positioned in other parts of the station. You need to get the numerous bunnies through the various rooms to the escape pods. Unfortunately, the corridors between the rooms can only fit so many bunnies at a time. What’s more, many of the corridors were resized to accommodate the LAMBCHOP, so they vary in how many bunnies can move through them at a time.
Given the starting room numbers of the groups of bunnies, the room numbers of the escape pods, and how many bunnies can fit through at a time in each direction of every corridor in between, figure out how many bunnies can safely make it to the escape pods at a time at peak.
Write a function solution(entrances, exits, path) that takes an array of integers denoting where the groups of gathered bunnies are, an array of integers denoting where the escape pods are located, and an array of an array of integers of the corridors, returning the total number of bunnies that can get through at each time step as an int. The entrances and exits are disjoint and thus will never overlap. The path element path[A][B] = C describes that the corridor going from A to B can fit C bunnies at each time step. There are at most 50 rooms connected by the corridors and at most 2000000 bunnies that will fit at a time.
For example, if you have:
entrances = [0, 1]
exits = [4, 5]
path = [
[0, 0, 4, 6, 0, 0], # Room 0: Bunnies
[0, 0, 5, 2, 0, 0], # Room 1: Bunnies
[0, 0, 0, 0, 4, 4], # Room 2: Intermediate room
[0, 0, 0, 0, 6, 6], # Room 3: Intermediate room
[0, 0, 0, 0, 0, 0], # Room 4: Escape pods
[0, 0, 0, 0, 0, 0], # Room 5: Escape pods
]Then in each time step, the following might happen:
0 sends 4/4 bunnies to 2 and 6/6 bunnies to 3
1 sends 4/5 bunnies to 2 and 2/2 bunnies to 3
2 sends 4/4 bunnies to 4 and 4/4 bunnies to 5
3 sends 4/6 bunnies to 4 and 4/6 bunnies to 5So, in total, 16 bunnies could make it to the escape pods at 4 and 5 at each time step. (Note that in this example, room 3 could have sent any variation of 8 bunnies to 4 and 5, such as 2/6 and 6/6, but the final solution remains the same.)
测试样例
1 | Input: |
题解
经典网络流,《挑战》上有原题,只是没有包装,在入流和出流分别加上一个总入流和总出流。
1 | def solution(entrances, exits, path): |
Level 4-2
题目
Running with Bunnies
You and the bunny workers need to get out of this collapsing death trap of a space station — and fast! Unfortunately, some of the bunnies have been weakened by their long work shifts and can’t run very fast. Their friends are trying to help them, but this escape would go a lot faster if you also pitched in. The defensive bulkhead doors have begun to close, and if you don’t make it through in time, you’ll be trapped! You need to grab as many bunnies as you can and get through the bulkheads before they close.
The time it takes to move from your starting point to all of the bunnies and to the bulkhead will be given to you in a square matrix of integers. Each row will tell you the time it takes to get to the start, first bunny, second bunny, …, last bunny, and the bulkhead in that order. The order of the rows follows the same pattern (start, each bunny, bulkhead). The bunnies can jump into your arms, so picking them up is instantaneous, and arriving at the bulkhead at the same time as it seals still allows for a successful, if dramatic, escape. (Don’t worry, any bunnies you don’t pick up will be able to escape with you since they no longer have to carry the ones you did pick up.) You can revisit different spots if you wish, and moving to the bulkhead doesn’t mean you have to immediately leave — you can move to and from the bulkhead to pick up additional bunnies if time permits.
In addition to spending time traveling between bunnies, some paths interact with the space station’s security checkpoints and add time back to the clock. Adding time to the clock will delay the closing of the bulkhead doors, and if the time goes back up to 0 or a positive number after the doors have already closed, it triggers the bulkhead to reopen. Therefore, it might be possible to walk in a circle and keep gaining time: that is, each time a path is traversed, the same amount of time is used or added.
Write a function of the form solution(times, time_limit) to calculate the most bunnies you can pick up and which bunnies they are, while still escaping through the bulkhead before the doors close for good. If there are multiple sets of bunnies of the same size, return the set of bunnies with the lowest worker IDs (as indexes) in sorted order. The bunnies are represented as a sorted list by worker ID, with the first bunny being 0. There are at most 5 bunnies, and time_limit is a non-negative integer that is at most 999.
For instance, in the case of
[
[0, 2, 2, 2, -1], # 0 = Start
[9, 0, 2, 2, -1], # 1 = Bunny 0
[9, 3, 0, 2, -1], # 2 = Bunny 1
[9, 3, 2, 0, -1], # 3 = Bunny 2
[9, 3, 2, 2, 0], # 4 = Bulkhead
]
and a time limit of 1, the five inner array rows designate the starting point, bunny 0, bunny 1, bunny 2, and the bulkhead door exit respectively. You could take the path:Start End Delta Time Status
- 0 - 1 Bulkhead initially open 0 4 -1 2 4 2 2 0 2 4 -1 1 4 3 2 -1 Bulkhead closes 3 4 -1 0 Bulkhead reopens; you and the bunnies exitWith this solution, you would pick up bunnies 1 and 2. This is the best combination for this space station hallway, so the solution is [1, 2].
测试样例
1 | Input: |
题解
这道题也是硬解的一道题,因为数据量不大,dfs后做了些剪枝过的,应该也不是正确解法。
- 首先用dp找到从i到j消费最少的路径
- 然后从start处开始dfs遍历所有可能的走法,以下为两个停止dfs的情况:
- 注意到这里会重复到bulkhead,最短路径原则至多到bulkhead n次
- 由于最终必须到达bulkhead,因此当前节点必须能走到bulkhead
1 | def solution(times, times_limit): |
Level 5
Level 5-1
这道题没做出来,感觉是dp,但没完全想出来
题目
Expanding Nebula
You’ve escaped Commander Lambda’s exploding space station along with numerous escape pods full of bunnies. But — oh no! — one of the escape pods has flown into a nearby nebula, causing you to lose track of it. You start monitoring the nebula, but unfortunately, just a moment too late to find where the pod went. However, you do find that the gas of the steadily expanding nebula follows a simple pattern, meaning that you should be able to determine the previous state of the gas and narrow down where you might find the pod.
From the scans of the nebula, you have found that it is very flat and distributed in distinct patches, so you can model it as a 2D grid. You find that the current existence of gas in a cell of the grid is determined exactly by its 4 nearby cells, specifically, (1) that cell, (2) the cell below it, (3) the cell to the right of it, and (4) the cell below and to the right of it. If, in the current state, exactly 1 of those 4 cells in the 2x2 block has gas, then it will also have gas in the next state. Otherwise, the cell will be empty in the next state.
For example, let’s say the previous state of the grid (p) was:
.O..
..O.
…O
O…To see how this grid will change to become the current grid (c) over the next time step, consider the 2x2 blocks of cells around each cell. Of the 2x2 block of [p[0][0], p[0][1], p[1][0], p[1][1]], only p[0][1] has gas in it, which means this 2x2 block would become cell c[0][0] with gas in the next time step:
.O -> O
..Likewise, in the next 2x2 block to the right consisting of [p[0][1], p[0][2], p[1][1], p[1][2]], two of the containing cells have gas, so in the next state of the grid, c[0][1] will NOT have gas:
O. -> .
.OFollowing this pattern to its conclusion, from the previous state p, the current state of the grid c will be:
O.O
.O.
O.ONote that the resulting output will have 1 fewer row and column, since the bottom and rightmost cells do not have a cell below and to the right of them, respectively.
Write a function solution(g) where g is an array of array of bools saying whether there is gas in each cell (the current scan of the nebula), and return an int with the number of possible previous states that could have resulted in that grid after 1 time step. For instance, if the function were given the current state c above, it would deduce that the possible previous states were p (given above) as well as its horizontal and vertical reflections, and would return 4. The width of the grid will be between 3 and 50 inclusive, and the height of the grid will be between 3 and 9 inclusive. The solution will always be less than one billion (10^9).
测试样例
1 | Input: |